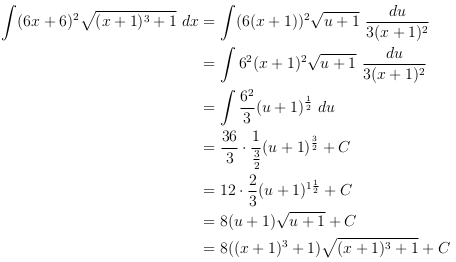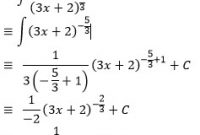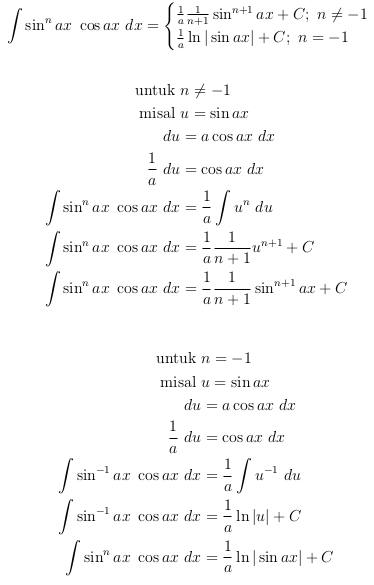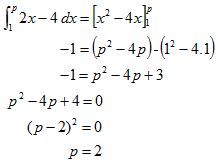Tentukanlah hasil dari. Teknik integral parsial ini digunakan bila suatu integral tidak dapat diselesaikan dengan cara biasa maupun dengan cara substitusi.
Integrasi Parsial Amp Substitusi Integral Tentu Tak Tentu
Contoh soal integral parsial dan substitusi. Rumus integral parsial juga digunakan untuk suatu soal integral yang sangat kompleks. Biasanya perlu metode yang tepat untuk menemukan hasil integralnya. Soal integral seperti diatas tidak bisa dikerjakan menggunakan rumus integral biasa. Sehingga diperoleh selain cara di atas dapat pula. Selain itu metode substitusi juga tidak bisa digunakan sebagai solusi untuk menemukan hasil integral dari soal yang disebutkan di atas. Disubstitusi dengan nilai u menjadi.
Biasanya cara ini digunakan untuk metode yang ada untuk menyelesaikan soal integral tidak bisa digunakan. Bentuk soal integral yang diberikan terkadang tidak bisa dikerjakan hanya menggunakan rumus integral secara biasa. Rumuscoid pada kesempatan kali ini kita akan membahas mengenai rumus integral parsial dan contoh soal beserta jawabannya dengan pembahasannya. Prinsip dasar integral parsial adalah sebagai berikut. Du 2 sin 2x dx. Integral merupakan cabang ilmu matematika yang memiliki tingkat kesulitan cukup tinggi.
Terdapat dua metode yang dapat digunakan dua metode tersebut adalah rumus integral substitusi dan rumus integral parsial. Demikianlah pembahasan mengenai contoh soal integral tentu tak tentu substitusi parsial dan rumus semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan kalian semua terima kasih banyak atas kunjungannya. Setelah sebelumnya kita membahas lengkap materi integral kali ini kita akan membahas contoh soal integral dengan menggunakan sifat sifat integral tentu dan tak tentusimak soal dan pembahasan berikut untuk meningkatkan pemahamanmu mengenai cara penyelesaian soal soal integral. Contoh dari soal integral yang bisa diselesaikan menggunakan rumus integral parsial adalah seperti dibawah ini. Contoh soal integral substitusi dan parsial dan pembahasan contoh soal 1.
Gallery of Contoh Soal Integral Parsial Dan Substitusi
