Contoh Soal Luas Daerah Yang Diarsir

Contoh soal 3. Guru sd smp sma contoh soal matematika luas daerah yang diarsir.

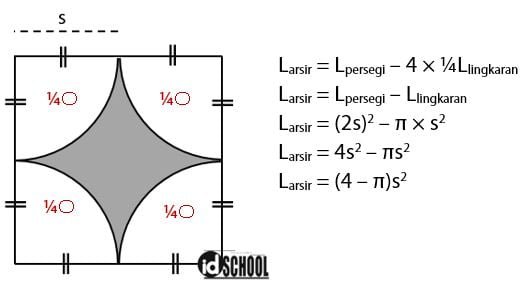
Menghitung Luas Daerah Yang Diarsir Idschool

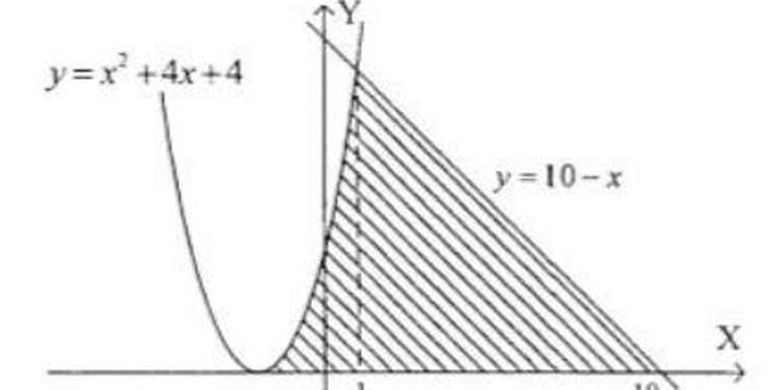
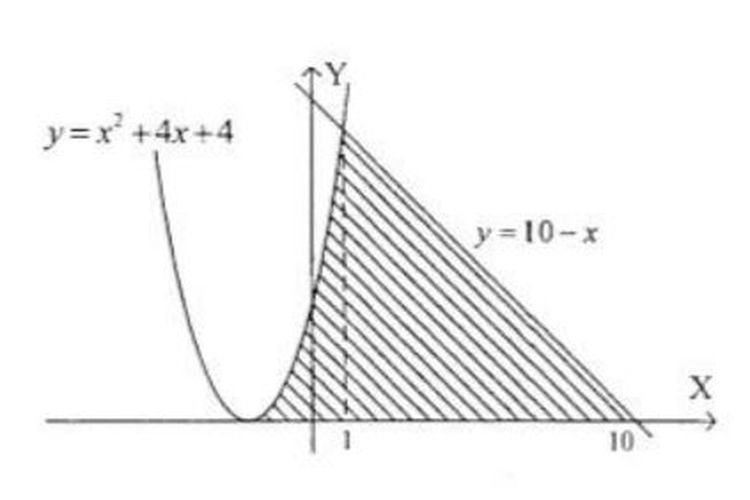
Contoh soal luas daerah yang diarsir. Batas integralnya adalah 4 dan 4. Contoh file soal uts lengkap kelas 1 6 sdmi semua mata pelajaran 20162017 berikut ini adalah kumpulan dari berbagi sumber tentang contoh soal matematika luas daerah yang diarsir yang bisa gunakan untuk bank soaldownloadsd dan diunduh secara gratis dengan menekan tombol download biru dibawah ini. Tentukan luas daerah yang diarsir berikut. Cari dan hitunglah luas segitiga tersebut. Luas daerah yang dibatasi kurva ditunjukkan oleh bagian yang diarsir. Contoh soal 4.

L 400 cm 2 jadi luas segitiga siku siku tersebut adalah 400 cm 2 contoh soal 3. T 40 cm. Baiklah setelah anda mengetahui dan memahami menghitung luas keliling dan diameter lingkaran maka alangkah baiknya jika anda langsung melihat contoh soal soal matematika yang bisa anda lihat beserta jawabanya langsung agar anda bisa lebih paham dan maksud akan rumusan yang ada pada tabel diatas. Berikut mafia online sajikan contoh soal tentang luas lingkaran yang diambil dari group matematika di facebook. Daerah gambar a dibatasi oleh fungsi linear garis lurus sehingga kita harus menentukan fungsi linearnya terlebih dahulu karena fungsinya belum ada. Mencari luas daerah yang dibatasi kurva aplikasi integral dapat ditemukan pada cara mencari luas daerah yang dibatasi kurva.

Sebelum mencoba memahami soal soal ini anda sebaiknya pahami terlebih dahulu konsep luas lingkaran dan keliling lingkaranjika sudah paham silahkan perhatikan contoh soal berikut ini. Soal tentang luas daerah un 2011 luas daerah yang dibatasi kurva y 4 x 2 y x 2 dan 0 x 2 adalah. Sebelum itu yang paling penting adalah pemahaman konsep rumus luas lingkaran karena konsep tersebut yang menjadi rumus dasar yang akan digunakan untuk menghitung luas daerah lingkaran yang diarsir. Jadi luas daerah yang diarsir adalah 2sqrt3 satuan luas. Pada bagian yang diarsir kurva fx lebih di atas dibandingkan dengan kurva gx maka luas daerah di atas bisa. L ½ x 20 x 40.

Baik yang dibatasi oleh sebuah kurva atau lebih. Sehingga luas daerah yang dibatasi kurva y x 2 16 adalah seperti berikut. Hitunglah luas daerah yang diarsir berikut ini. Misalkan persamaan garis kita tulis menjadi fx 2x 17 dan parabola menjadi gx x 2 25. Jadi luas daerah yang dibatasi kurva y x 2 16 dengan sumbu x adalah 52 satuan luas. Ada sebuah segitiga tumpul yang memiliki panjang alasnya 10 cm dan juga memiliki tinggi4 cm.

L ½ x a x t. Contoh soal yang belum diketahui fungsinya. A 20 cm. Jika sudah paham konsepnya maka kita dapat menghitung luas daerah dengan berbagai macam dan tidak mengalami kesulitan. Jadi luas daerah yang diarsir pada gambar tersebut dapat dinyatakan dengan rumus pada opsi c. Selain itu aplikasi integral juga digunakan untuk mencari volume benda putar yang merupakan daerah yang dibatasi kurva kemudian diputar 360 o mengelilingi sumbu x atau sumbu y.

Tanda negatif menunjukkan bahwa daerah luas berada di bawah sumbu x. Luas daerah yang diarsir adalah jawab.