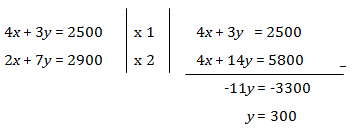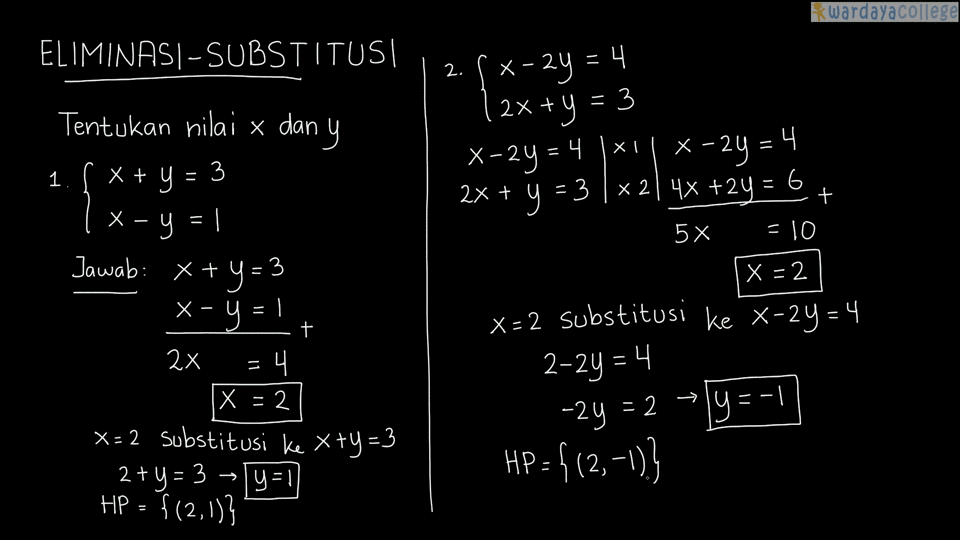Tentukan himpunan penyelesaian dari sistem persamaan berikut dengan metode substitusi jika x y variabel pada himpunan bilangan real. Metode substitusi digunakan karena tidak semua fungsi dapat diintegralkan dengan rumus dasar atau metode anti turunan sesuai dengan defenisinya.

Contoh Penyelesaian Sistem Persamaan Dua Variabel Dalam
Contoh soal metode substitusi. Berikut ini materi lengkap tentang integral substitusi dan integral parsial mulai dari konsep dasar teknik tekniknya rumus contoh soal pembahasan. Adapun langkah langkah untuk menyelesaikan spldv dengan metode subtitusi adalah sebagai berikut. 2x 3y 5. Untuk memantapkan pemahaman anda tentang metode substitusi silahkan simak contoh soal berikut ini. Nah pada kesempatan kali ini kita akan membahas tentang cara menentukan himpunan penyelesaian hp sistem persamaan linear dua variabel dengan menggunakan metode subtitusi. Di sini kamu akan belajar tentang metode substitusi melalui video yang dibawakan oleh bapak anton wardaya.
Di sini kamu akan belajar tentang metode eliminasi substitusi melalui video yang dibawakan oleh bapak anton wardaya. Dan selanjutnya akan diberikan beberapa contoh soal untuk memantapkan pengetahuan temen temen. Kumpulan soal mudah sedang sukar. Silakan perhatikan contoh soal di bawah ini agar lebih jelas. X 3y 7. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Tentukan nilai x dan y dari persamaan berikut ini. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal. 4x y 8 dan x 2y 10. Contoh soal dan pembahasan 2. Walaupun tidak semua soal dapat diselesaikan dengan metode substitusi tetapi adanya teknik ini sangat membantu menyelesaikan soal soal trigonometri yang cukup rumit. Metode substitusi merupakan cara menyelesaikan persamaan linear dengan memasukan salah satu persamaan kedalam persamaan yang lain.
Salah satu persamaan harus diubah menjadi x atau y masukkan persamaan yang sudah diubah itu ke persamaan lainnya. Pada metode substitusi langkah pengerjaannya adalah. Kumpulan soal mudah sedang sukar.