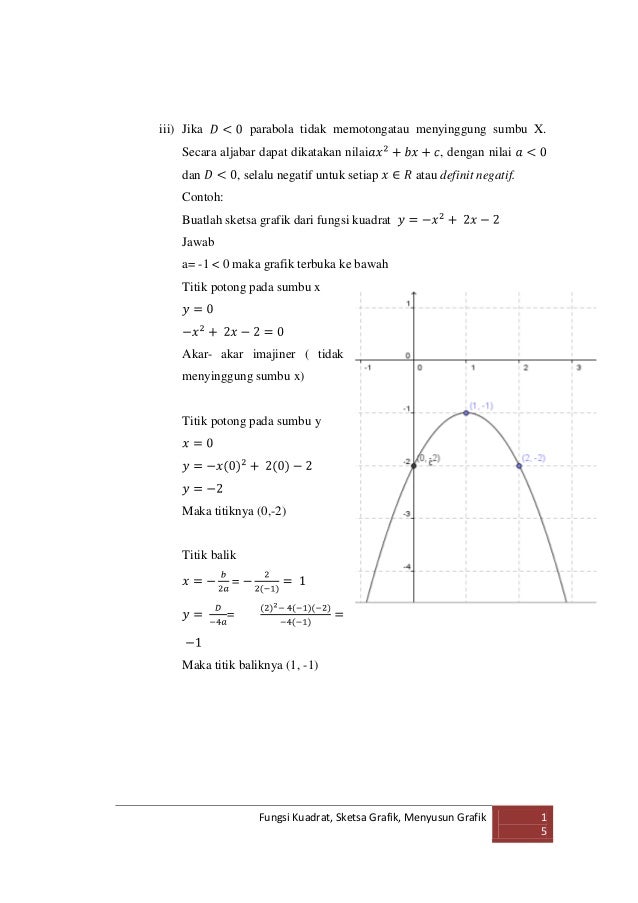
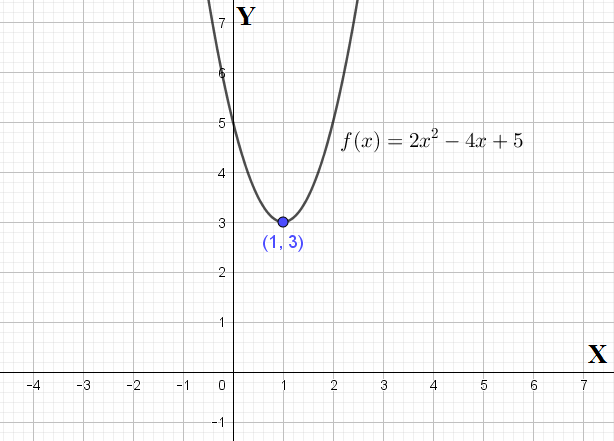Tidak menutup kemungkinan sejumlah siswa sulit memahami materi tersebut sehingga penulis. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
Fungsi Kuadrat Grafik Rumus Menyusun Persamaan Contoh Soal
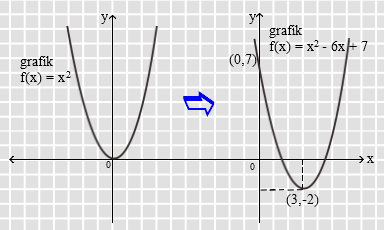
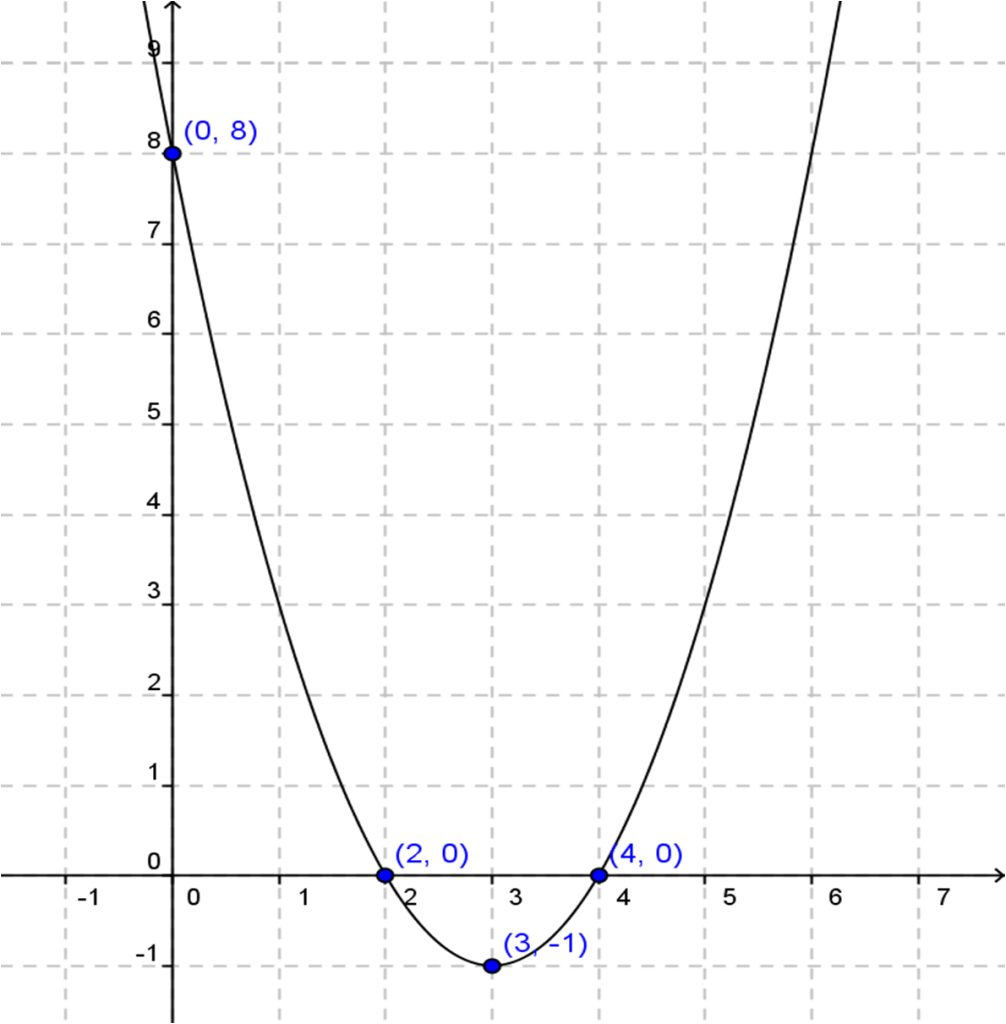
Contoh soal persamaan grafik fungsi kuadrat dan penyelesaiannya. Jika fungsi kuadrat diketahui titik potong dengan sumbu x yaitu x 1 0 dan x 2 0 maka persamaannya adalah fx ax x 1 x x 2 b. Fungsi kuadrat merupakan salah satu materi yang dipelajari pada tingkat smasederajat. Mari kita bedah bersama fungsi kuadrat dari fxx 2 6x8. Misalkan a b c r dan a 0 maka persamaan yang terbentuk. Ingat titik potong dengan sumbu x akan didapatkan apabila nilai y0 maka dari itu akan didapatkan bentuk persamaan kuadrat x 2 6x80. Bentuk umum persamaan kuadrat.
Grafik fungsi kuadrat dalam bidang cartesius dikenal sebagai parabola. Umumnya materi ini dipelajari setelah siswa memahami konsep mengenai persamaan kuadrat karena selain melibatkan perhitungan secara aljabar materi ini juga melibatkan analisis secara geometri gambar grafik. Dinamakan persamaan kuadrat dalam peubah x. Kemudian pasangan nilai x y tersebut menjadi koordinat dari yang dilewati suatu grafik. Untuk mengerjakan soal soal yang berkaitan dengan fungsi kuadrat kita harus memahami konsep dasar dalam fungsi kuadrat meliputi bentuk umum fungsi kuadrat itu sendiri nilai diskriminan fungsi kuadrat dan bagaimana pengaruh nilai tersebut terhadap bentuk dan sifat grafik fungsi kuadrat dan cara menggambar grafik fungsi kuadrat. Persamaan kuadrat adalah persamaan yang hanya memuat satu peubah atau variabel dan pangkat tertinggi dari variabel tersebut adalah 2.
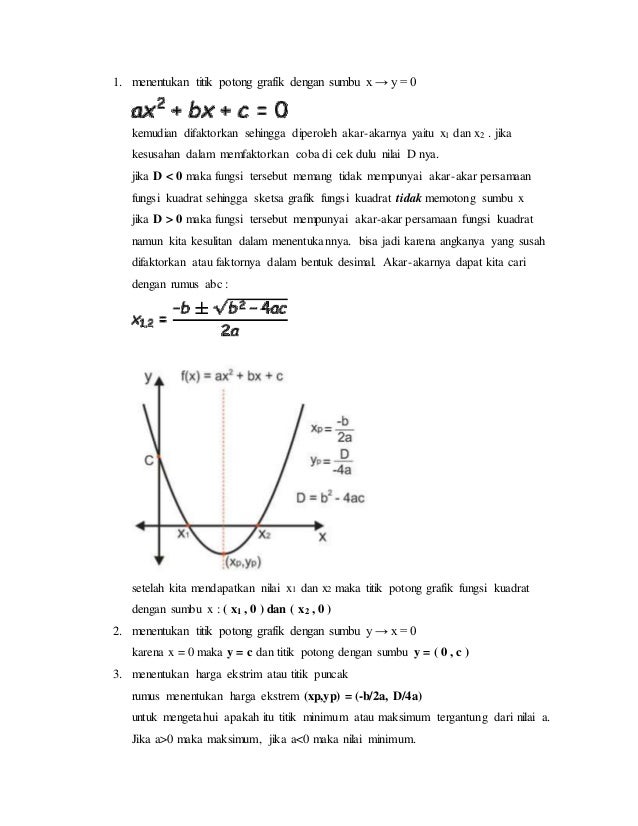
Titik potong dengan sumbu x. Ax 2 bx c 0. ƒx ɑx 2 bx c a b dan c r ɑ 0 untuk semua nilai x dalam daerah asalnya. Sebagai contoh grafik dari fungsi. Postingan ini membahas contoh soal persamaan kuadrat dan penyelesaiannya atau pembahasannya. Fungsi kuadrat juga dikenal sebagai fungsi polinom atau fungsi suku banyak berderajat dua dalam variabel x.
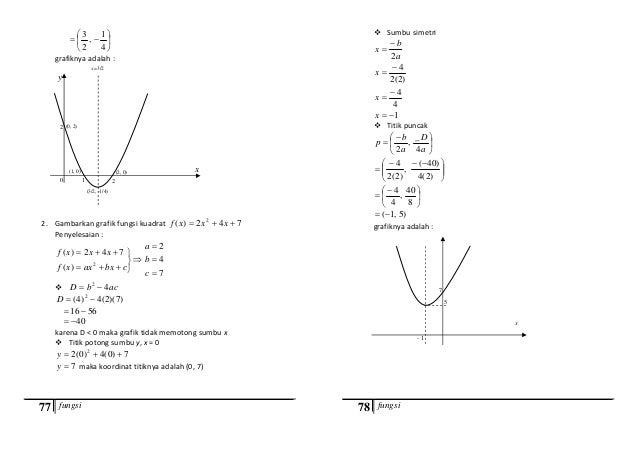
Jika suatu fungsi kuadrat diketahui titik baliknya pp q maka persamaannya adalah fx ax p 2 q untuk lebih jelasnya ikutilah contoh soal berikut ini. Menentukan akar akar persamaan kuadrat ada beberapa cara diantaranya. X 2 6x 9 0 x 3 x 3 0 x 3 0 atau x 3 0 x 3. Untuk memastikan bahwa persamaan kuadrat di atas mempunyai akar maka langkah pertama adalah menentukan terlebih dahulu diskriminannya. Bentuk umum fungsi kuadrat. Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y.
Gallery of Contoh Soal Persamaan Grafik Fungsi Kuadrat Dan Penyelesaiannya
