Apabila nilai dari r 2 adalah 100 misalnya pada regresi linier sederhana semua titik darai data yang diteliti akan menempel pada garis regresi sehingga jika semakin kecil nilai dari r 2 maka data tersebut makin menyebar jauh dari garis regresi. Academiaedu is a platform for academics to share research papers.
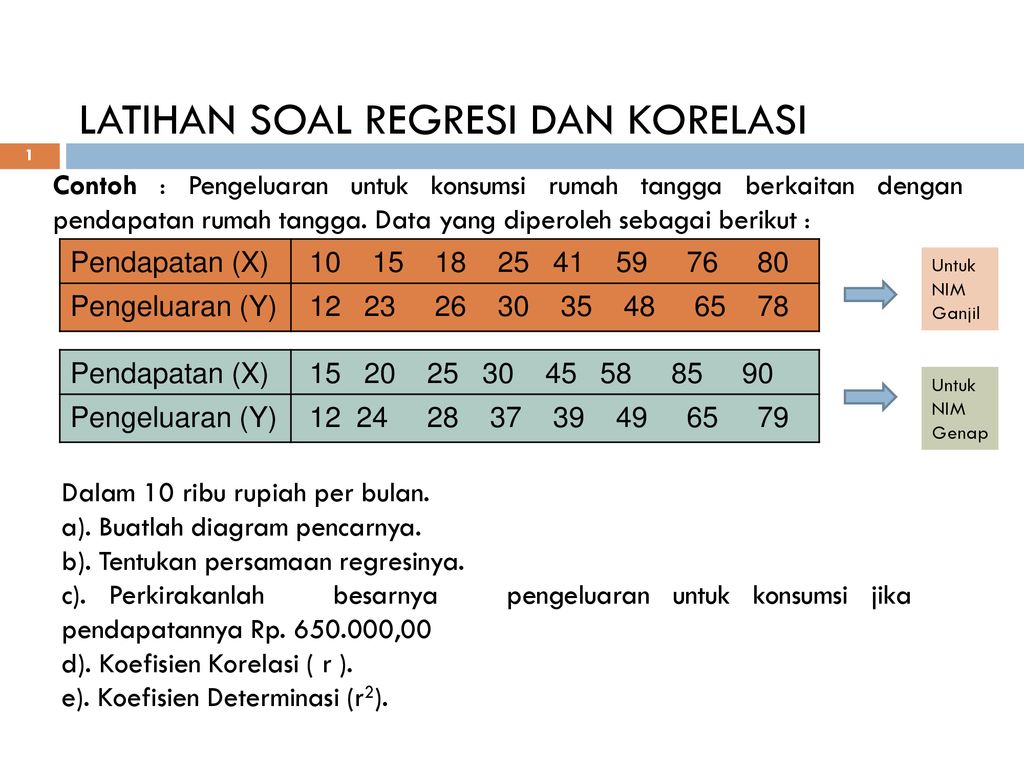
Latihan Soal Regresi Dan Korelasi Ppt Download
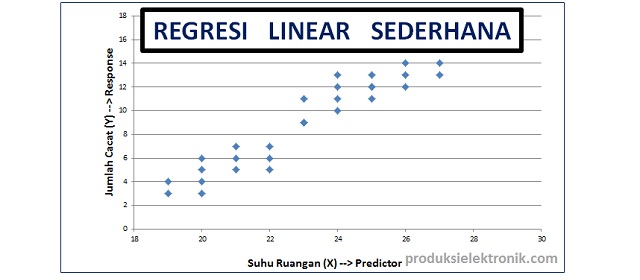
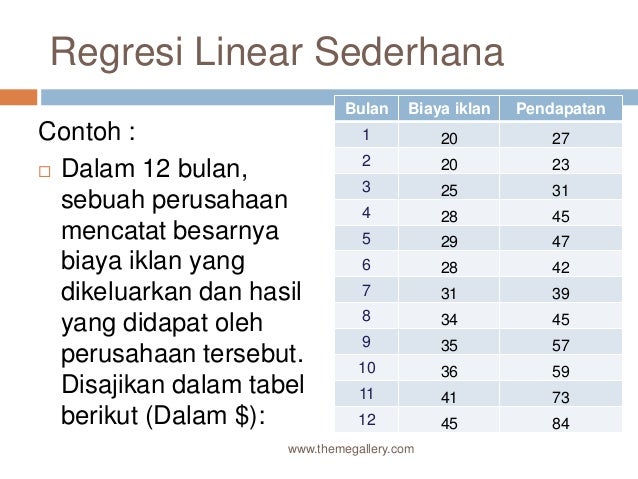
Contoh soal regresi linier. Y a b x maka persamaan regresi dalam soal ini adalah. Diketahui suatu penelitian terhadap hubungan antara nilai biaya periklanan dengan tingkat penjualan dari sebuah koperasi adalah sebagai berikut. Istilahregresi yang berarti ramalan atau taksiran pertama kali diperkenalkan oleh sir francis galton pada tahun 1877. Menentukan persamaan regresi linier sederhana. Menentukan besarnya koefisien korelasi dan koefisien determinasi. Regresi linier sederhana adalah suatu metode yang digunakan untuk melihat bentuk hubungan antar satu variabel independent bebas dan mempunyai hubungan garis lurus dengan variabel dependennya terikat.
Regresi ganda dengan 3 variabel bebas. Y 936 27 x b. Menentukan persamaan regresi linier sederhana. Contoh kasus analisis regresi linear sederhana. Sebuah variabel hasil observasi yang diperoleh sangat mungkin dipengaruhi oleh variabel lainnya misalkan tinggi badan dan berat badan seseorang. Contoh soal regresi linier berganda dalam suatu penelitian yang dilakukan terhadap 10 rumah tangga yang diilih secara acak diperoleh data pengeluaran untuk pembelian barang barang tahan lama per minggu y pendapatan per minggu x 1 dan jumlah anggota rumah tangga x 2 sebagai berikut.
Y 936 27 x b. Y a b x maka persamaan regresi dalam soal ini adalah. Soal sebuah penelitian dilakukan untuk menetukan apakah ada hubungan antara jangka waktu pengeringan dengan berkurangnya berat suatu bahan yang dikeringkandiperoleh data sebagai berikut jangka waktu pengeringan jamberat yang berkurang mg12101089210110131200790088210930675099111105 tentukan persamaan regresi linier sederhana. Analisis regresi linear sederhana regresi linear sederhana adalah metode statistik yang berfungsi untuk menguji sejauh mana hubungan sebab akibat antara variabel faktor penyebab x terhadap variabel akibatnyafaktor penyebab pada umumnya dilambangkan dengan x atau disebut juga dengan predictor sedangkan variabel akibat dilambangkan dengan y atau disebut juga dengan response. Pengertian dan contoh kasus uji regresi linear sederhana dan berganda regresi merupakan suatu alat ukur yang juga digunakan untuk mengukur ada atau tidaknya korelasi antarvariabel.